Lesson 1: Solubility of Salts

Part a: The Solubility Product Constant, K_sp

Part a: The Solubility Product Constant, K_sp
Part b: Solubility and K_sp
Part c: Solubility and Common Ion Effects

 

The Big Idea

A lot of chemistry occurs in aqueous solutions. A good deal of it is only understood by applying equilibrium principles to the substances that are dissolving in water. The need for an equilibrium model is best demonstrated by the dissolving of insoluble salts in water and the chemistry of weak acids and weak bases. In Lesson 1, we will examine the first topic - the dissolving of insoluble salts, with an emphasis on the mathematics. In Lesson 2, we will look at the mathematics of acid-base chemistry in aqueous solutions.
 
 

Soluble vs. Insoluble Salts

Salts are ionic compounds formed from ionic bonding between a cation and an anion. Many salts dissolve in water and are considered soluble. Other salts are regarded as insoluble due to their tendency towards minimal solubility. Whether a salt falls into one category or the other is largely dependent upon the ions that it is composed of. Experimental studies of numerous compounds have led to rules for predicting the solubility of compounds in water based on the ions that are present. These rules are known as solubility rules.
 
A list of solubility rules is shown below. The rules can be used to predict if an ionic compound will dissolve in water. If a compound dissolves, it will be in the (aq) state. If it does not dissolve when dumped in water, it will remain in the solid state – (s) state. Observe that there are exceptions to many of the rules. The list does not include every ion; but it does include those ions most commonly encountered in an introductory Chemistry course.
 

 
In Lesson 1, our focus will be on the insoluble salts. We will learn that even soluble salts dissolve ... just a little bit. Sometimes, a wee little bit. The best term to describe such salts is slightly soluble or sparingly soluble. Since “just a little bit” and “a wee little bit” are not the most scientific of terms, we will learn strategies for quantifying the degree to which they dissolve.

 

 
 

Dissociation of Salts

All salts, whether soluble or insoluble will dissociate when they dissolve. They break apart or split up into separate ions. The ions that are formed by the dissociation are the ions you hear when you say the compound’s name. Calcium chloride dissociates into calcium ions (Ca²⁺) and chloride ions (Cl^-). Potassium sulfate dissociates into potassium ions (K⁺) and sulfate ions (SO₄^2-). Barium phosphate dissociates into barium ions (Ba²⁺) and phosphate ions (PO₄^3-). The names, formulae, and charges of these ions has been discussed elsewhere in this Chemistry Tutorial. Success in this chapter will require a comfort with the topic. If necessary, use the links to refresh your understanding.

Names and Formulae of Ionic Compounds:  Binary | Containing Polyatomic Ions

 
The dissociation of a salt is represented by a dissociation equation. The equation shows the undissociated salt as the reactant in the solid state. As it dissolves, it also dissociates. The products are the two ions in the aqueous state. Coefficients are added where necessary to balance the equation. Here are a few examples of dissociation equations for ionic compounds.

CaCl₂(s)  →  Ca²⁺(aq)  +  2 Cl^-(aq)
 
K₂SO₄(s)  →  2 K⁺(aq)  +  SO₄^2-(aq)
 
Ba₃(PO₄)₂(s)  →  3 Ba²⁺(aq)  +  2 PO₄^3-(aq)

Success in this chapter will also require some fluency with writing dissociation equations. We devoted a page to the topic in our Solutions Chapter. If necessary, visit Dissociation of Ionic Compounds.
 
 
 

A New Model for Insoluble Salts

A rather simplified model of soluble salts is to think of them dissociating to completion. Add 1.0 mole of NaCl(s) to a liter of solution, and there will be 1.0 mole of Na⁺(aq) ions and 1.0 mole of Cl^-(s) ions. It completely dissociates, provided the amount of solid added is at or below its solubility limit (which for NaCl, is approximately 6.0 moles per 1 L of water).
 
A rather simplified model of insoluble salts is to think of them as not dissolving. Add 1.0 mole of AgCl to a liter of solution and there will be 1.0 mole of AgCl(s) at the bottom of the beaker. The simplified model takes insoluble quite literally, translating it to mean that none of it dissolves at all and there are no ions in solution. The more accurate model has a different narrative that goes like this: Add 1.0 mole of AgCl to a liter of solution and there will be 1.3x10^-5 mole of Ag⁺(aq) ions and 1.3x10^-5 mole of Cl^-(s) ions dissolved in the solution. This model views the so-called insoluble salt as being ever-so-slightly soluble or sparingly soluble.

 

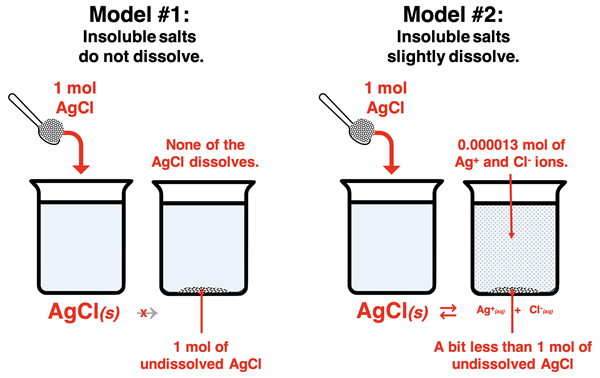
 It is this second model that we will attempt to build in Lesson 1. It differs from the first model in a number of ways:

• Insoluble salts are slightly soluble, sparingly soluble, or ever-so-slightly soluble.
• Insoluble salts in water are accompanied by dissolved ions in the solution.
• The dissociation is a reversible process described by the reversible reaction arrow (⇄).
• There are people who can predict and calculate the amount of solid that dissolves. (These people are called Chemistry students.)

 
 

Case Study: Dissolving SnI₂ in Water

Let’s do a thought experiment with tin(II) iodide, a reddish-orange solid. According to some sources, it falls in the insoluble salt category. It so happens that SnI₂ dissolves to a greater extent than other salts in this insoluble category. Its solubility is 0.029 mol per liter of water at 25°C. It dissociates as follows:
   
Let’s suppose we start with a beaker filled with 1.0 L of water. Suppose that we add 3.7 g of SnI₂, approximately 0.010 moles. It will completely dissolve, resulting in 0.010 mol Sn²⁺(aq) and 0.020 mol I^-(aq). There will be no solid remaining in the beaker since we are far below the solubility limit of 0.029 mol/L. See Trial 1 in the table below.
 
The same observations would be observed if we added 0.020 mol SnI₂ and 0.025 mol SnI₂. All the solid would dissolve and dissociate into ions. Only ions would be present in the solution. See Trials 2 and 3.
 
Now suppose we add 0.030 mol of SnI₂ to the 1.0 L of water. This is slightly above the solubility limit of 0.029 mol/L. At this point, some undissolved solid would remain in the beaker and the Sn²⁺(aq) and I^-(aq) ion concentrations would be 0.029 M and 0.058 M. See Trial 4.
   
What would happen if more solid was added to the water? Would this cause more dissolving? Trials 5 and 6 display the answers. No! The solubility limit was reached at 0.029 moles of SnI₂ in 1.0 L of water. The solution has become saturated with ions and no more ions can be dissolved in the solution. Adding more solid does not increase the concentration of ions. The additional solid added beyond the solubility limit would begin to accumulate as undissolved solid at the bottom of the beaker.
   
 
As you can see, insoluble solids do dissolve! It’s just that the solubility limit is rather low. They are slightly soluble or sparingly soluble. And it should be emphasized that we selected SnI₂, a solid that has a high limit for those that fall into the category of insoluble. If our thought experiment included lead(II) iodide as our solid, the solution would have become saturated upon addition of approximately 0.0014 mole of PbI₂ in a 1.0 L of water. And if we have picked silver chloride, the solution would have become saturated after the addition of 0.000013 mole of AgCl in 1.0 L of water. The solubility limit is dependent upon the actual solid (and the temperature). This is true for both soluble and insoluble salts. But for those that we classify as insoluble, the limit is very small. (In Lesson 1b, you will learn how to calculate it.)
 
 
 

The Equilibrium Model of Insoluble Salts

In Trial 4 of our tin(II) iodide thought experiment, the solution was saturated with Sn²⁺ and I^- ions. Additionally, there was some undissolved solid present in the beaker. At this point, there is an equilibrium system formed between the undissolved solid and the dissolved ions. Like any equilibrium system, it is a dynamic state in which two opposing processes are balanced. The opposing processes can be labeled as dissociation and precipitation. Both processes occur at the same rate on the surface of the solid. The solid is dissociating into aqueous state ions and the aqueous state ions are combining to join the particles of solid at the beaker’s bottom. For this reason, the dissolving of the solid in water is represented by an equation with the reversible reaction arrow:
   
Like any reversible system, there is an equilibrium constant that describes the relationship between reactant and product concentrations. The rules for equilibrium constant expressions were discussed in Chapter 14 of our Chemistry Tutorial. In the next section, we will apply those rules to the dissolving of insoluble salts in water.
 
 
 

The Solubility Product Constant

The equilibrium model to mathematically analyze the dissolving of insoluble salts in water. Each reaction has its own unique equilibrium constant – a numerical value that is dependent upon temperature. This equilibrium constant is referred to as the solubility product constant and represented by the symbol K_sp. The table below shows K_sp values at 25°C for several selected salts.
   
As is always the case, an equilibrium constant provides a measure of the extent to which the reaction occurs. In general, salts with larger K_sp values will dissolve to a greater extent than those with smaller K_sp values. (As we will find out in Lesson 1b, the number of ions produced by the dissociation also impacts the solubility of the solid.)
 
 
 

Writing K_sp Expressions

The K_sp value is the equilibrium constant for the dissolving of an insoluble salt. The equilibrium constant value is equal to the equilibrium constant expression for the reaction. As discussed in Chapter 14, the expression is the ratio of product to reactant concentrations, each raised to a power equal to its coefficient. Only gaseous- and aqueous-state reactants and products are included in the expression. Pure solids and liquids are omitted. When applied to dissociation reactions, the solid reactant is not included. The K_sp value is equal to product of the two ion concentrations, each raised to a power equal to its coefficient. Here are three examples:
 
For the dissociation of silver chloride, AgCl:
   
For the dissociation of lead(II) iodide, PbCl₂:
   
For the dissociation of barium phosphate, Ba₃(PO₄)₂:
   
 
As always, see our Check Your Understanding for some personal practice.
  
   
 

How to Determine Ion Concentrations for Insoluble Salts

The following method can be used to determine the ion concentrations from the K_sp value.

1. Write the balanced chemical equation for the dissociation of the solid.
2. Write the K_sp equation for the reaction.
3. Set up an ICE table. Use the variable x to represent the amount of solid that dissolves.
4. Substitute the K_sp value and the expressions for the equilibrium concentrations of the ions (x, 2x, 3x, etc.) into the K_sp equation.
5. Use algebra to solve for the x and for the ion concentrations.

 
We will demonstrate the method with two examples. Additional (and more complicated) examples are included in Lesson 1b.
 
 
 

Example 1 - Determining Ion Concentrations

The K_sp for silver chloride is 1.8x10^-10 at 25°C. Determine the ion concentrations at equilibrium.
 

Solution:

 
 

Example 2 - Determining Ion Concentrations

The K_sp for lead(II) sulfate is 1.6x10^-8 at 25°C. Determine the ion concentrations at equilibrium.
 

Solution:

 
 
 

Next Up

Examples 1 and 2 included simple salts having 1:1 ion ratios with simple dissociation equations having coefficients of 1  This means the equilibrium concentrations were raised to the first power. It also means that the algebra was a little more straightforward. In Lesson 1b, we will solve similar problems with non 1:1 ion ratios and more difficult algebra. We will also relate the results to the concept of solubility. But before you advance forward, take some time to put your learning into practice with the suggestions in the Before You Leave section.
 
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Insoluble Salts and K_sp. Save it to a safe location and use it as a review tool. (Coming Soon.)

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. An insoluble salt is one that is best understood as being a solid that ______.

1. will not dissolve in water whatsoever
2. will not mix with water in any way
3. will ever-so-slightly dissolve in water
4. will fully dissolve in water without limits.

 
2. The difference between soluble salts and insoluble salts is that _____.

1. soluble salts dissolve in water and insoluble salts don’t dissolve in water
2. soluble salts have been stirred into the water and insoluble salts have not yet been added to the water
3. soluble salts dissolve completely in water without any limits on the amount and insoluble salts dissolve in water but there are limits on how much can dissolve
4. soluble salts have relatively high limits of solubility and insoluble salts have relatively low limits on their solubility

​


 
3. Use the list of Solubility rules to identify the following salts as being soluble or insoluble. For each decision, identify the rule (#1-8) that you used.
a. MgCl₂


b. KC₂H₃O₂
​

c. Al(OH)₃
​

d. AlPO₄
​

e. BaSO₄
​

f. PbCl₂ 
​


 
4. Consider the thought experiment involving the dissolving of SnI₂ that was discussed earlier on this page: 

SnI₂(s)  ⇄  Sn²⁺(aq)  +  2 I^-(aq)

The equilibrium concentrations of ions were: [Sn²⁺] = 0.029 M and [I^-] = 0.058 M.
a. Write the K_sp equation for this system.

b. Use equilibrium concentrations to calculate the K_sp value for SnI₂.


c. If the K_sp value were a smaller number, would the equilibrium concentrations be smaller or larger than the 0.029 M and 0.058 M values? Explain.


 
 
5. Suppose that we do a thought experiment with the insoluble salt, PbI₂, similar to the thought experiment for SnI₂. PbI₂ dissociates as

PbI₂(s)  ⇄  Pb²⁺(aq)  +  2 I^-(aq)

Its solubility is approximately 0.0014 mol/L. Five trials are performed with increasing amounts of PbI₂ in each trial. The data for the mass and moles of the PbI₂ added to 1.0 L of water are shown. Use your understanding to complete the table.

 
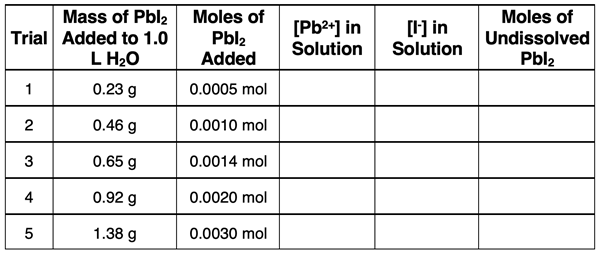
Match each beaker diagram below with one of the five trials.

 
 
6. For the following insoluble salts, write the dissociation equation for its dissolving in water and write the K_sp equation.
a. PbBr₂

b. CuCO₃


​c. Fe(OH)₃


​d. Ag₂SO₄


​
 
7. The K_sp for calcium sulfate is 4.5x10^-5 at 25°C. Use the five steps to determine the ion concentrations at equilibrium.



​